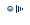Пошук в ширину
Метод пошуку в ширину дає найкоротший шлях від вихідного стану до цільового в просторі станів.
Пошук цільового стану проходить зразу по всіх напрямках . Нехай в нас є дерево станів.
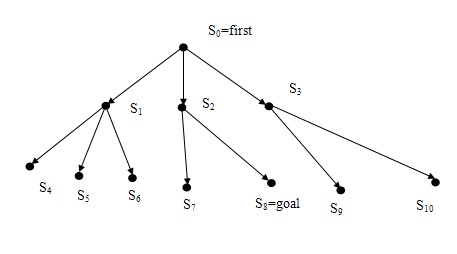
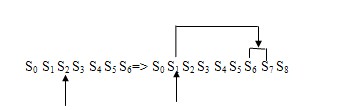
Нехай S0 – початковий стан, а S8 – шуканий стан. При розв’язуванні задач, зазвичай організовують чергу станів і знову породжені стани поміщують в хвіст черги. Цільовий стан, якщо такий досягнуто, знаходиться в хвості черги. Пояснимо утворення цієї черги. Почнемо з початкового стану S0=first і встановимо на нього показник. З стану S0 можна перейти в один з станів S1, S2, S3, тому поміщаємо їх в хвіст черги.
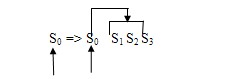 Потім
перетягуємо вказівник. Тепер вказівник вказує на другий елемент черги S1. З S1 можна перейти на S4 , S5,
S6 , тому дописуємо ці
елементи в хвіст черги.
Потім
перетягуємо вказівник. Тепер вказівник вказує на другий елемент черги S1. З S1 можна перейти на S4 , S5,
S6 , тому дописуємо ці
елементи в хвіст черги.
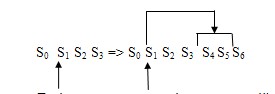 Далі
пересовуємо вказівник на третій елемент черги S2 і дописуємо в хвіст черги S7 , S8. Стан S8 – цільовий,
тому пошук на цьому завершується.
Далі
пересовуємо вказівник на третій елемент черги S2 і дописуємо в хвіст черги S7 , S8. Стан S8 – цільовий,
тому пошук на цьому завершується.
Однак можлива і інша ситуація. Могло статися так, що вказівник досяг кінця черги, а цільового значення не досягнуто і нові стани не породжуються. Можливий ще один випадок, коли черга станів нескінченно подовжується, а цільового значення досягнути неможливо. Строго говорячи, при розв’язуванні задачі методом пошуку в ширину потрібно довести неможливість виникнення такої ситуації. Одним із застосувань пошуку в ширину є алгоритм Лі або хвильовий алгоритм.
Задача. Дано кліткове поле. Частина клітинок занята перешкодами. Необхідно попасти з деякої клітинки в другу задану шляхом послідовного переміщення по клітинках. Рухатись можна тільки на одну клітинку вгору, вправо, вниз або вліво.
Розв’язання.
Позначимо перешкоди 1, а клітинки по яких можна ходити 0. Кліткове поле буде являти собою прямокутний масив. Розширимо заданий масив двома стовпцями і двома рядками (по периметру) і заповнимо додаткові рядки і стовпці одиницями, щоб краї поля ототожнити з перешкодами. Поставимо в початкову клітинку число 2. Занесемо координати початкової точки у створену чергу. У всі вільні клітинки навколо початкової заповнимо числом 3. Координати цих клітинок занесемо в хвіст черги. Всі вільні клітинки біля трійок заповнимо числом 4, заносячи відповідні координати в хвіст черги і так далі поки хвиля чисел не досягне кінцевої клітинки, або не закінчиться черга. Нехай координати початкової клітинки 9, 3, а кінцевої 2, 10.
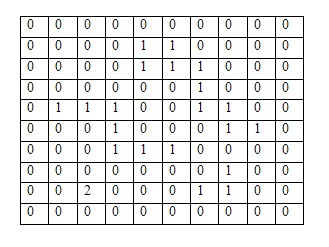
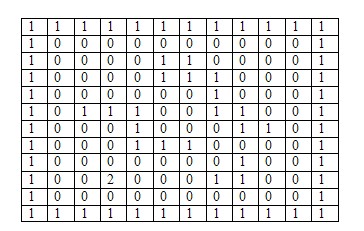
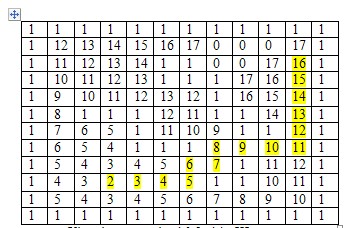
Кількість
кроків 16-2=14. Шлях знаходять рухаючись з кінцевої точки до початкової в
сторону зменшення чисел.
1. Задача «ОЗЕРО» (20 балів)
Ім’я вхідного файлу: OZERO.DAT
Ім’я вихідного файлу: OZERO.SOL
Максимальний час роботи на одному тесті: 5с
Прямокутне озеро задається матрицею N x M (4<=N<=M<=100) і вкрите островами. В лівому верхньому кутку знаходиться пліт розміром 1 х 1. За один крок пліт може рухатися на одну клітину по вертикалі або горизонталі. Знайти найменший шлях плоту до правого нижнього кутка. Якщо шляхів декілька, то вивести один із них.
Вхідні дані.
Перший рядок файлу OZERO.DAT містить два числа N і M. Далі у наступних рядках знаходиться план озера, на якому 1 позначені острови, а 0 – вільний водяний простір.
Вихідні дані.
Послідовність координат (1,1), ... , (N, M) (без пробілів).
Приклад вхідного файлу OZERO.DAT
5 6
0 0 1 0 0 0
0 0 0 0 1 0
0 1 1 1 0 0
0 1 0 0 0 1
0 0 0 1 0 0
Приклад вихідного файлу OZERO.SOL
Розв’язок задачі.
#include <fstream>
ifstream in("OZERO.DAT");
ofstream out("OZERO.SOL");
int main()
{
int n,m;
in>>n>>m;
int a[102][102],//лабіринт
cherga[10000][2],//черга
dx[]={-1,0,1,0},// зміна рядка
dy[]={0,1,0,-1},// зміна стовпця
xn,yn,//координати початку
xk,yk,//координати кінця
i,j,//поточна точка
vkp,/*вказівник на початок черги */ vkk,/*вказівник на кінець черги*/
t;
bool y; // перевіряє чи досягнуто кінця
for (i=1;i<=n;i++) // ввід лабіринту з файла
{
for (j=1;j<=m;j++)
in>>a[i][j];
}
for (i=0;i<=n+1;i++)
{
a[i][0]=1; //заповнення нульового стовпчика одиницями
a[i][m+1]=1; //заповнення додаткового стовпчика одиницями
}
for (i=0;i<=m+1;i++)
{
a[0][i]=1; //заповнення нульового рядка одиницями
a[n+1][i]=1;//заповнення додаткового рядка одиницями
}
xn=1; yn=1; //початкова точка
xk=n; yk=m; //кінцева точка
a[xn][yn]=2;
vkp=0; //Вказівник читання з черги
vkk=1; //вказівник запису в чергу
y=false;
cherga[1][0]=xn;
cherga[1][1]=yn;
while ((vkp<vkk)&&(!y))//пока черга не порожня і не знайдено рішення
{
//за вказівником читання беремо елемент з черги
vkp++; i=cherga[vkp][0]; j=cherga[vkp][1];
if ((i==xk) && (j==yk)) y=true; //якщо це клітинка виходу з лабіринту, то розв’язок знайдено
else
for (t=0;t<=3;t++)
if (a[i+dx[t]][j+dy[t]]==0)
{ //в цій клітинці ми ще не були
a[i+dx[t]][j+dy[t]]=a[i][j]+1;
//присвоїмо значення мітки
vkk++;
cherga[vkk][0]=i+dx[t];
cherga[vkk][1]=j+dy[t]; //Записуємо координати клітинки в чергу
};
}
int b[10000][2],//масив для запису шляху
k=0;//лічильник елементів
i=xk;j=yk; //кінцеву точку робимо поточною
b[0][0]=xk; b[0][1]=yk;//записуємо її в масив
while ((i!=xn) || (j!=yn))// поки не досягнута початкова точка
{
for (t=0;t<=3;t++) //перевірка сусідніх точок, тобто пошук меншої на 1
if (a[i][j]-a[i+dx[t]][j+dy[t]]==1)
{
i=i+dx[t]; j=j+dy[t]; //знайдену точку робимо поточною
k++; b[k][0]=i; b[k][1]=j;
};
}
for (i=k;k>0;k--)//виводимо шлях, враховуючи, що він у масиві в оберненому порядку
{
out<<"("<<b[k][0]<<","<<b[k][1]<<"),";
}
out<<"("<<b[k][0]<<","<<b[k][1]<<")"<<"\n";
}